
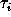 /
/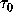 ) correction because the echo is
proportional to 1/t and is integrated up to the time
) correction because the echo is
proportional to 1/t and is integrated up to the time 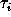 when
inelastic scattering processes destroy the phase coherence of
the two complementary waves and the echo disappears. As a
consequence the conductance is reduced and the resistance is
increased, both by the same fraction
when
inelastic scattering processes destroy the phase coherence of
the two complementary waves and the echo disappears. As a
consequence the conductance is reduced and the resistance is
increased, both by the same fraction 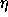 . A similar argument can
be made in real space where the coherent back-scattering yields
the same correction
. A similar argument can
be made in real space where the coherent back-scattering yields
the same correction 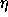 to the diffusion constant D. And since the
conductance is proportional to the diffusion constant one
obtains the same conductance corrections
to the diffusion constant D. And since the
conductance is proportional to the diffusion constant one
obtains the same conductance corrections 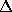 G
G

This is not the end of the story, nature is even more
generous. If we apply a magnetic field perpendicular to the film
then our electron wave picks up a magnetic phase shift. For a
closed loop this phase shift is equal to e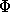 /
/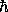 where
where 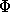 is the
enclosed magnetic flux, and e the charge of the electron. Since
our two complementary waves (along the closed loop) surround the
flux in opposite direction their magnetic phase shifts have
different signs and the two amplitudes have no longer the same
phase. When their combined phase shift is of the order of one
they no longer interfere constructively.
is the
enclosed magnetic flux, and e the charge of the electron. Since
our two complementary waves (along the closed loop) surround the
flux in opposite direction their magnetic phase shifts have
different signs and the two amplitudes have no longer the same
phase. When their combined phase shift is of the order of one
they no longer interfere constructively.
Let l be the mean free path of the electrons and 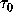 the time between two collisions. Now we consider an electron on a closed
loop with n scattering events. This electron returns after the
time t=n
the time between two collisions. Now we consider an electron on a closed
loop with n scattering events. This electron returns after the
time t=n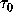 to its starting point. (With t we denote the time
which an electron needs to diffuse along a closed loop). Of
course, there are many different closed loops with n scattering
events. Each of these closed loops encloses an area F. The size
of F for the different closed loops lies between -n
to its starting point. (With t we denote the time
which an electron needs to diffuse along a closed loop). Of
course, there are many different closed loops with n scattering
events. Each of these closed loops encloses an area F. The size
of F for the different closed loops lies between -n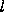 ²
and +n
²
and +n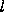 ² where n
² where n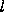 ²=2Dt.
(In two dimensions the diffusion constant has the
value D=
²=2Dt.
(In two dimensions the diffusion constant has the
value D=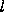 ²/2
²/2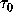 .)
In a magnetic field H the resulting phase shift
.)
In a magnetic field H the resulting phase shift
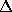
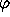 between two complementary waves
has a Gaussian distribution with a width of 2eFB/
between two complementary waves
has a Gaussian distribution with a width of 2eFB/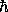
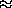 4DBt. For t>1/4DB there are closed loops
with constructive and others with destructive interference. In
an average the interference cancels out. For t<1/4DB, on the
other hand, the phase shift between complementary waves is
sufficiently small that the interference remains constructive.
This means that in a given magnetic field we roughly
accumulate the echo up to a time t=1/4DB. If we plot now the
resistance as a function of 1/B then the 1/B axis is equivalent
to a time axis.
4DBt. For t>1/4DB there are closed loops
with constructive and others with destructive interference. In
an average the interference cancels out. For t<1/4DB, on the
other hand, the phase shift between complementary waves is
sufficiently small that the interference remains constructive.
This means that in a given magnetic field we roughly
accumulate the echo up to a time t=1/4DB. If we plot now the
resistance as a function of 1/B then the 1/B axis is equivalent
to a time axis.
In Fig.4 we have plotted the resistance of a Mg film (upper curve) as a function of 1/B in a semi-logarithmic plot. The corresponding time scale is indicated at the top of the figure. In our experiments the field B=1T is equivalent to a time of 0.3 ps. The ordinate, i.e. the resistance, represents (besides a constant) the integrated echo (corresponding to the number of sailors who returned up to a time t to the bar). On a logarithmic time scale the integrated echo is a linear function. For B<0.01T (which corresponds to t>30ps) the curve becomes flat. Here the diffusion time is so large that electron phonon processes destroy the coherence of the two complementary waves. The length of the coherent echo can be extended by lowering the temperature of the film sample.