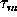 ) where dt/
) where dt/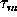 is the chance that a sailor is mugged during the time dt.
is the chance that a sailor is mugged during the time dt.So far this real life experiment appears to be a one shot or pulse experiment because we assumed that all the sailor left the bar at the same time. That is not necessary. If the sailors leave the bar at arbitrary times the bouncer may register the departure time t0 of each sailor. If he has a good memory for faces then he recognizes at what time t1 the individual sailors return. If we plot now the number of returning sailors as a function of t=t1-t0 we obtain the same function as before.
Electrons in a metal film with scattering centers
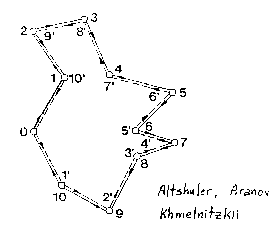
In our physics experiments the city is a thin (two- dimensional) metal film, the sailors are the electrons in the film, the street corners are scattering centers (for example, lattice defects) where the electrons change their direction randomly. In Fig.2 we follow the path of such an electron. (Of course, the position of the scattering centers is random). We consider a path which is a closed loop. The first question is how do we count the electrons (who plays the bouncer) and how do we distinguish a returning electron from another one which comes from somewhere else? In contrast to sailors electrons do not have faces.

Instead we use the fact that the electrons propagate as a waves and have a well defined phase. Consider in Fig.2 an electron wave which propagates from 0 via 1, 2, 3, .. back to 0. (This path is generally called a Feynman path and its meaning is well defined). Being a wave the electron can, at the same time, also propagate from 0 via 10, 9, 8, .. back to 0 on the reversed path. We call these two partial electron waves "complementary". Both partial waves return to 0 with exactly the same amplitude A, including its phase. At point 0 the two complementary waves interfere. The combined return probability of the two complementary waves is |2A|²=4|A|². For two uncorrelated electron waves this return probability has only the value 2|A|². Therefore we have an additional "coherent back scattering" of 2|A|². Its size is (as for the sailors) proportional to 1/t. We find this constructive interference only when the electron propagates along a closed loop. Therefore we see that we can well distinguish the returning electron from other electrons which come from elsewhere. Of course, we have many closed loops along which the electron can propagate. We find this coherent back-scattering for each closed loop. (However, the electron phases for different loops are uncorrelated and their interference cancels in an average).